29th

计算机如何存储浮点数

IEEE-754 标准中定义了计算机如何用 32 个比特位存储一个浮点数：从左边起，第 1 位是符号位，用 s 表示，s=0 表示正数，s=1 表示负数；第 2 位到第 9 位是指数位，用 e 表示；第 10 位到第 32 位是有效数位，用 f 表示。知道了s、e、f，根据下面的公式，就可以算出浮点数的值：

$(−1)^s×1.f×2^{e-127}$

e 为啥要减 127 呢？因为 e 是 8 位，能表示 0 ~ 255 之间的整数，那么「e - 127」的范围就是 -127 ~ 128，不过由于 e = 0 和 e = 255 时有特殊用途，所以，e - 127 实际的范围是 -126 ~ 127。你可能会问，为什么指数部分不用二进制补码来表示负数，而是用「e 减去 127」这种方式？第一是因为 e = 0 时有特殊用途，没法用于补码；第二是因为采用「减去一个固定值」的方式更容易进行浮点数之间大小的比较。

上面这个公式是没法表示 0 的，所以 IEEE 规定，当 e = 0 且 f = 0 时，就认为这个浮点数是 0。还有其他一些特殊情况，见下表：

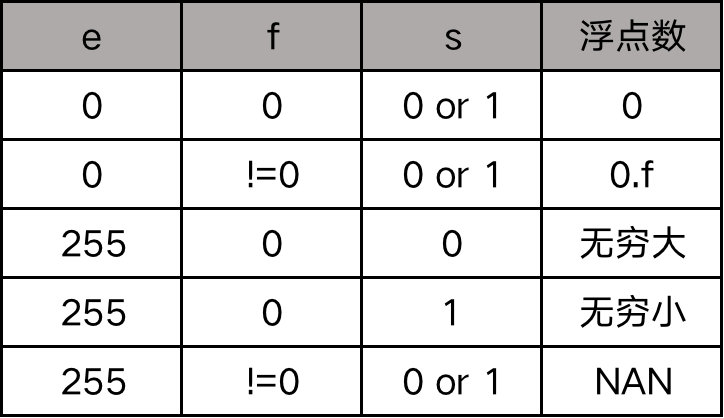
看到上面的公式，你可能会感到疑惑，1.f 是二进制数，但是 $2^e$ 不是二进制数（二进制数里面只有 0 和 1），那这个公式应该怎么算？其实可以这样，如果你想要二进制数，就根据 e 去移动 1.f 中的小数点，当 e>0 时，小数点向右移动，当 e<0 时，小数点向左移动，e 是几就移动几位，移动完小数点就得到了二进制的浮点数；如果你想要十进制数，就把 1.f 转成十进制，然后按照十进制的规则去计算 $2^e$ ，最后把两者相乘，就得到了十进制的浮点数。（无论是二进制还是十进制，都不要忘了前面的符号位）

比如下面这个浮点数

s = 0，e = 126，所以 e - 127 = -1，f = 0，所以它表示的二进制浮点数是： $(-1)^0\times 1.0 \times 2^{-1}=0.1$ ，十进制就是 $(-1)^0\times 1.0 \times \frac{1}{2}=0.5$ （十进制中 $2^{-1}=\frac{1}{2}$ ）

这种用 32 个比特位表示的浮点数我们称之为单精度浮点数，即 float，还有一种用 64 个比特位表示的浮点数，我们称之为双精度浮点数，即 double。double 的指数位长度是 11，有效数位长度是 52，所以 double 能够表示的数的范围更广，精度更高。

下图为 double 的各区域的长度。

由于 double 的指数位长度变成了 11，所以计算 double 浮点数的值的公式变成了 $(−1)^s×1.f×2^{e-1023}$

浮点数之所以叫浮点数，是因为它的小数点是浮动的，小数点后面的有效数由 e 和 f 共同决定。除了浮点数，还有定点数，即小数点后的位数是固定的，最典型的定点数就是 BCD 编码。

下次说一下为什么在编程语言中用 float 类型的 0.3 + 0.6，结果会是 0.899999…，而不是 0.9。

参考资料：

1. 极客时间 -《深入浅出计算机组成原理》第 15 讲、第 16 讲

2. https://www.h-schmidt.net/FloatConverter/IEEE754.html

3. 《计算机组成与设计：硬件 / 软件接口》3.5.1 节